From τὰ φυσικά (ta physika) to physics – IX

In the episode in this series on Aristotle I wrote:

It is important to note, for the evolution of scientific thought in Europe throughout the centuries after Aristotle, that when applied to nature he didn’t regard mathematical proofs as valid. He argued that the objects of mathematics were not natural and so could not be applied to nature. He did however allow mathematics in what were termed the mixed sciences, astronomy, statics, and optics. For Aristotle mathematical astronomy merely delivered empirical information on the position of the celestial bodies. Their true nature was, however, delivered by non-mathematical cosmology. 

In the next three episodes I will be taking a separate look to the three so-called mixed sciences–astronomy, optics, statics–starting with astronomy, because all three would go on to play a significant role in the development of physics in the Early Modern Period.

We have already seen that Aristotle propagated a homocentric, mathematical, astronomical model of the cosmos that was originally conceived by Eudoxus of Cnidus (c. 390–c. 340 BCE), and then further developed by Callippus (c. 370–c. 300 BCE) and Aristotle himself. However, we don’t have any real astronomical texts from any of the three. In what follows I shall be looking at the work of the practical astronomers Hipparchus (Greek: Ίππαρχος, Hipparkhos) (c. 190–c. 120 BCE) and Ptolemaeus (Greek: Πτολεμαῖος, Ptolemaios, English: Ptolemy), which basically means the work of Ptolemaeus, as most of what we know about Hipparchus is taken from the Geographica of Strabo (63 BCE–c. 24 CE), the Naturalis Historia of Plinius (23–79 CE), and Ptolemaeus’ Mathēmatikē Syntaxis or Almagest as it is more commonly known.

Although Ptolemaeus was one of the most influential scholars in antiquity we know almost nothing about him. He appears to have lived and worked in the city of Alexandria during the second century CE and that is quite literally all we know.

Sixteenth century engraving of Ptolemaeus being guided by the personification of astronomy, Astronomia – Margarita Philosophica by Gregor Reisch, published in 1508. Ptolemaeus is shown wearing a crown, as during the Middle Ages, he was thought falsely to be part of the ruling Ptolemaic dynasty Source: Wikimedia Commons

19th-century engraving of Hipparchus Source: Wikimedia Commons

We have exactly the same problem with Hipparchus who was born in Nicaea, which is now in Turkey, and is said to have died in Rhodes. The dates given for his life are guestimates based on the known dates of some of his astronomical observations. 

Starting with Ptolemaeus’ Mathēmatikē Syntaxis, what this represents is a fully fledged science in the modern sense but which in its development goes back more than a thousand years. The Mathēmatikē Syntaxis is a vast collection of empirical data, which is then analysed to produce a mathematical model of the observable celestial sphere. It is in this sense no different to the astronomical work of Copernicus or Tycho Brahe and the only thing that separates from the work of John Flamsteed, in the time of Newton, is that much of Flamsteed’s empirical data was acquired with a telescope, an instrument that the earlier astronomer did not have available to them. 

A 14th.century Greek manuscript of the Mathēmatikē Syntaxis; it shows a table layout, and the functions of the columns, colours and rows are labelled in this depiction. Source: Wikimedia Commons Manuscript source

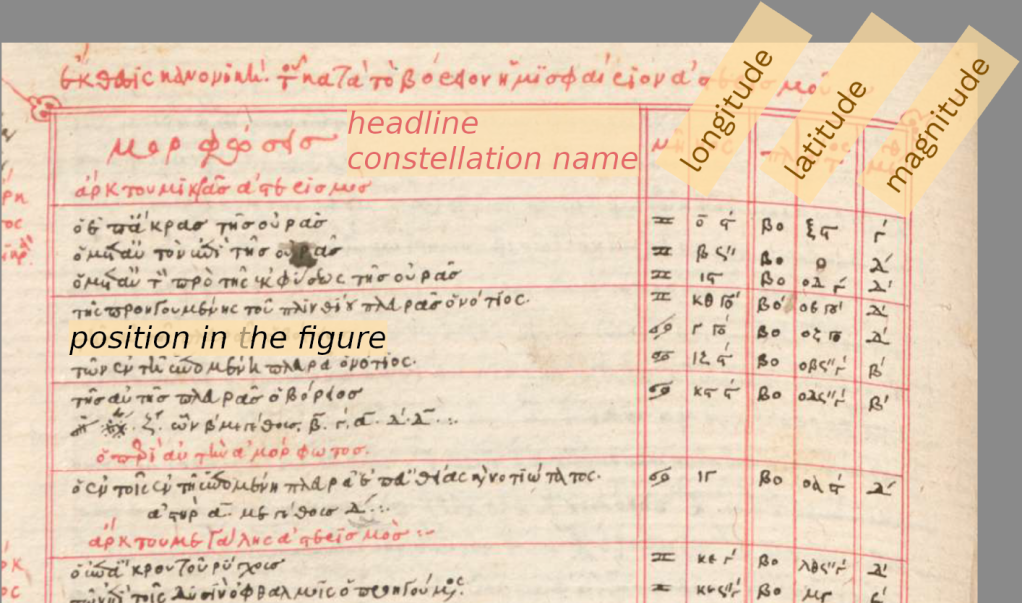
The Mathēmatikē Syntaxis was published sometime in the middle of the second century CE. It was translated into Arabic in total five times starting around eight hundred. Islamic astronomers studied, analysed, and criticised it. They added new mathematical methods to improve it, but they did nothing to change its fundamental structure.

Arabic Almagest beginnings of the star catalogue Source

It was translated both from the original Greek and from Arabic into Latin in the twelfth century, again without major change.

Claudius Ptolemaeus, Almagestum, 1515 Full manuscript Source

In the fifteenth century Peuerbach and Regiomontanus produced their Epitome of the Almagest, for Cardinal Bessarion, an updated, modernised, shortened, mathematically improved version of the Almagest.

Epytoma Ioannis de Monte Regio in Almagestum Ptolomei, Latin, 1496 Full manuscript source

The basic concept and structure, however, remained the same and this, in its printed version from 1496, became the standard advanced astronomy textbook in Europe. Copernicus, who learnt his astronomy from the Epitome of the Almagest, and modelled his De revolutionibus (1543) on it. The Mathēmatikē Syntaxis was and remained the archetype for a general presentation of astronomy. 

Ptolemaeus’ model is a geocentric one for the obvious reason that it best fitted the available empirical data. As far as the observer is concerned there is no indication that the earth moves in anyway whatsoever, it’s a stable non-moving platform, as far as the observer can tell. This is what makes the mental leap to a heliocentric model so extraordinary. However, even within a heliocentric paradigm astronomical observation remain by definition geocentric until the late twentieth century when the human race made its first tentative steps into space.

Why am I saying this? There is a widespread misconception that somehow Copernicus created a completely new astronomy when he published his De revolutionibus, in reality he didn’t, he ‘merely,’ where merely is doing a lot of work, hypothesised a new model within the astronomical frame that Ptolemaeus had given him in his Mathēmatikē Syntaxis. Tycho Brahe did nothing other with his geo-heliocentric model. The observational astronomy remains the same the mathematical interpretation of the acquired data changes. 

Regiomontanus, Wilhelm IV of Hesse-Kassel, and Tycho Brahe all recognised that the data set delivered up in the Mathēmatikē Syntaxis had become corrupted by constant copying of manuscripts and all set about creating new data but using the same basic techniques and instruments as Ptolemaeus. Regiomontanus died before his programme really got of the ground but both Wilhelm and Tycho created new accurate data sets. Tycho developed another new interpretation of the data with his geo-heliocentric model.

A simplified, short explanation of the emergence of modern science during the Early Modern Period is that the qualitative natural philosophy of Aristotle was replaced by a quantitative natural philosophy in which empirical data was analysed and interpreted mathematically. The oft quoted mathematisation of science of which Newton’s Principia Mathematica is held up as the prime example. Ptolemaeus’ Mathēmatikē Syntaxis already offered up a role model for this way of doing science. However, because Aristotle had claimed that mathematics does not or cannot describe reality the Mathēmatikē Syntaxis was generally interpreted, but not as we will see by Ptolemaeus, as being merely a calculating device to determine the position of the celestial object for astrology, cartography, navigation, etc. This, of course, changed with Copernicus, as astronomers began to regard their mathematical models as describing reality. Astronomy became one of the principle driving forces behind the seventeenth-century mathematisation of science.

I’m not going to give a detailed analysis of everything that is in the thirteen books of the Mathēmatikē Syntaxis. I would need a whole blog series for that. However, I will make some salient points of what Ptolemaeus delivers in his complete package. 

In the first book he describes a basically Aristotelian image of the cosmos. The Earth a sphere at the centre of a spherical cosmos. Without mentioning either Aristarchus of Samos, who is credited by a couple of sources with having proposed a heliocentric cosmos, or Heraclides Ponticus (c. 390–c. 310 BCE), who proposed a geocentric system with diurnal rotation, Ptolemaeus criticises those who would attribute diurnal rotation to the Earth, anticipating a common criticism of Copernicus. He argues quite logically that if the Earth was rotating on its axis the resulting headwind would cause havoc. Copernicus opposed this argument correctly by claiming that the Earth carries its atmosphere with it in a sort of envelope but couldn’t explain how this physically functioned. Much of the history of physics of the seventeenth century are the incremental steps towards supplying the solution to this problem, culminating in Newton’s theory of universal gravitation.

Ptolemaeus deviates strongly from Aristotelian philosophy in two important aspects. Firstly, it is fairly obvious that he regards his mathematical models as describing reality and not just being a method of calculating the positions of celestial objects. This is something that tended to be ignored by the medieval Aristotelian philosophers, who used the Mathēmatikē Syntaxis. Secondly, because it was not capable of explain all of the properties of the planetary orbits, he abandoned the homocentric spheres model replacing it with variations on an deferent /epicycle model, combined with an eccentric, i.e., the deferent is not centred on the Earth but a point some distance away from it, and with the uniform circular motion measured from an equant point, an abstract point equidistant from the eccentric point as the Earth.

Ptolemaeus’ model of the planetary orbits

This complex geometrical construction led several times down the century to a rejection of the Ptolemaic astronomy and the demand for a return to the Aristotelian homocentric astronomer. The last attempt being by Girolamo Fracastoro (c. 1477–1553) and Giovanni Battista Amico (1511? – 1536), Fracastoro’s book Homocentricorum sive de stellis (Homocentric [Spheres] or Concerning the Stars) being published in 1538, just five years before De revolutionibus. 

Portrait of Girolamo Fracastoro by Titian, c.1528 Source: Wikimedia Commons

Ptolemaeus was by no means the originator of all that is contained in his Mathēmatikē Syntaxis, which is a presentation of accumulated astronomical knowledge produced over a couple of thousand years. The most extreme view held by some historians is that he stole or plagiarised all of it from Hipparchus. Others are less drastic in their judgement. However, there is no doubt that he owed a major debt to Hipparchus, which he partially acknowledges.

The story, however, does not begin with Hipparchus. European astronomy has its principal roots in the astronomy of the Babylonians, who began systematic observations of the celestial sphere because of their astrological belief that the heavens controlled/affected life on Earth. Over the centuries they accumulated a vast amount of astronomical data out of which they developed accurate models to predict the movements of the celestial bodies. Unlike the Greeks, these were not geometrical models but numerical algorithms. They also developed an accurate algorithm to predict lunar eclipses. They also had an algorithm to predict when a solar eclipse might take place but could not predict whether it would or not. 

Around five hundred BCE, the Greeks took over both the Babylonian astronomy and astrology. They developed both further and changed from algebraic to geometrical models of the celestial movements. Hipparchus at some point almost certainly produced something resembling the Mathēmatikē Syntaxis, which included, amongst other things, a significant star catalogue, giving the observed positions of numerous stars. Ptolemaeus’ most extreme critics accuse him of having taken his entire star catalogue, of 1022 stars, from Hipparchus and didn’t observe any himself.

Hipparchus’ greatest contribution is that he is credited with having produced the first trigonometrical table. This was a table of chords, whereby in a unit circle the chord of an angle is twice the sine of half of the angle. Ptolemaeus used a standard circle with a diameter of 120 so, chord 𝛉 = 120 sin(𝛉/2). Ptolemy includes a chord table giving values for angles from 0.5 to 180 degrees in 0.5 degree intervals and follows it with an introduction to spherical trigonometry. Improved, first by the Indian astronomer, who introduced the sine, and then by Islamic astronomers, whose work then entered Europe, where it was further developed, trigonometry became an important part of the mathematical canon in the Early Modern Period.                          

Like the Babylonians, Ptolemaeus’ astronomy was closely related to his astrology. He wrote what would become the standard astrological text, his Tetrabiblos (Τετράβιβλος) ‘four books’, also known in Greek as Apotelesmatiká (Ἀποτελεσματικά). In this work he stated that the science of the stars, astrologia, has two aspects: 

One, which is first both in order and in effectiveness, is that whereby we apprehend the aspects of the movements of sun, moon, and stars in relation to each other and to the earth, as they occur from time to time. [The Mathēmatikē Syntaxis]  

The second is that in which by means of the natural character of these aspects themselves we investigate the changes which they bring about in that which they surround. [The Tetrabiblos].

In the Early Modern Period the Tetrabiblos was as influential in academic circles as the Mathēmatikē Syntaxis. 

Opening page of Tetrabiblos: 15th-century Latin printed edition of the 12th-century translation of Plato of Tivoli; published in Venice by Erhard Ratdolt, 1484.

For the astrologers and other users of astronomical data Ptolemaeus produced his Handy Tables (Ptolemaiou Procheiroi kanones), to quote historian of Ancient Greek astronomy, Alexander Jones:  

Ptolemy’s Handy Tables, the corpus of astronomical tables that he produced after completing the Almagest, largely adapting them from the tables embedded in that treatise, was a work of immense importance in later antiquity and in the medieval traditions of the Eastern Mediterranean and the Middle East. If the Almagest was the primary transmitter of the theoretical foundations of Greek mathematical astronomy, the Handy Tables was par excellence the practical face of that astronomy. 

The Handy Tables were at least as influential as the Mathēmatikē Syntaxis during late antiquity and also during the Islamic Middle Ages.

Ptolemaeus also wrote a cosmology, the Planetary Hypotheses (Greek: Ὑποθέσεις τῶν πλανωμένων, lit. “Hypotheses of the Planets”). This is a physical realisation of the cosmos with his deferent/epicycle models of the planetary orbits embedded in the Aristotelian crystalline spheres. With the orbits determining the inner and outer surfaces of the spheres, Ptolemaeus was thus able to determine the dimensions of the cosmos. He estimated the Sun was at an average distance of 1,210 Earth radii, much too low, as we now know, while the radius of the sphere of the fixed stars was 20,000 times the radius of the Earth. 

No Greek of Latin manuscript of the Planetary Hypotheses is known from antiquity, and it was long thought to be a lost work. In the fifteenth century, the Austrian astronomer, Georg von Peuerbach (1423–1461), produced his Theoricae Novae Planetarum (New Planetary Theory), which was the first book printed and published by his pupil Regiomontanus (1436–1476), in 1473, and it was the first ever mathematical/scientific book to be printed with movable type. This work of cosmology was, together with the Peuerbach’s and Regiomontanus’ Epitome of the Almagest, the textbook from which Copernicus learnt his astronomy. The Theoricae Novae Planetarum also presents Ptolemaeus’ deferent/epicycle models of the planetary orbits embedded in the Aristotelian crystalline spheres and was for several hundred years thought to be an original work by Peuerbach.

Peuerbach Theoricae novae planetarum 1473 Source: Wikimedia Commons

In the 1960s a previously unknown Arabic manuscript of Ptolemaeus’ Planetary Hypotheses was discovered, and it was obvious that Peuerbach’s work was an updated version of Ptolemaeus’, just as the Epitome of the Almagest was an updated version of the Almagest.

Ptolemaeus was also authored his Geōgraphikḕ Hyphḗgēsis, which became known in Latin as either the Geographia or Cosmographia, together with the Mathēmatikē Syntaxis and the Tetrabiblos it forms an interrelated trilogy of books. The Geōgraphikḕ Hyphḗgēsis is in different ways related to both books. It and the Mathēmatikē Syntaxis both use a longitude and latitude system; the Mathēmatikē Syntaxis to map the heavens, Geōgraphikḕ Hyphḗgēsis to map the Earth. However, they differ slightly, as Ptolemaeus uses and ecliptical system for the heavens and an equatorial one for the Earth. Hipparchus had used an equatorial system to map the heavens. It is important to note that the latitude/longitude system of mapping was first devised to map the celestial sphere and only later brought down to Earth to map the globe. Ptolemaeus adds in his Geōgraphikḕ Hyphḗgēsis that using astronomy is the best way to determine longitude and latitude for cartography. On a superficial level the three books are connected by the fact that one needs to know the latitude of a subject’s place of birth in order to cast their horoscope. However, for Ptolemaeus the connection between astrology and geography goes much deeper. Ptolemaeus thought that each of the four quarters of the Earth was connected to one of the four astrological triplicities–

Fire (Aries, Leo, Sagittarius), characteristics: hot, dry – the north-west quarter Europe

Earth (Taurus, Virgo, Capricorn), characteristics: cold dry – the south-eastern quarter Greater Asia

Air (Gemini, Libra, Aquarius) characteristics: hot, wet – the north-eastern quarter Scythia

Water (Cancer, Scorpio, Pisces) characteristics: cold, wet – the south-western Ancient Libya

These connections determined the general characteristics of each area and the population that lived there.

Jacobus Angelus’ Latin translation of Ptolemaeus’ Geographia Early 15th century Source via Wikimedia Commons

The Geōgraphikḕ Hyphḗgēsis was translated into Arabic by the nineth century and had a major impact on Islamic cartography. However, unlike the Mathēmatikē Syntaxis and the Tetrabiblos it was not translated into Latin in the twelfth century but first in 1406 by Jacobus Angelus. It had a fairly direct influence on European cartography changing the European approach to map making extensively and also very importantly, the need to accurately determine longitude and latitude, done astronomically as Ptolemaeus had recommended, was a major driving force in the attempts to reform astronomy, one aspect of which was Copernicus’ heliocentric system. That reform movement was also driven by a desire for more accurate astronomical data to improve astrological prognostications, due to rising status of astrology particularly in astro-medicine.

Often in popular literature written off as the out dated representative of an ignorant geocentric astronomy, Ptolemaeus’ publications actually had a major impact on and played a significant role in the renewal and modernisation of science in the fifteenth, sixteenth and seventeenth centuries that usually gets called the scientific revolution. 

Finding your way underground

The Renaissance is a period of intense mathematical activity, but it is not mathematics as somebody who has studied mathematics at school today would recognise it but rather practical mathematics, that is mathematics developed and utilised within a particular practical field of work or study. It should be emphasised that this is not what we now know as applied mathematics, which is, as its name suggests, the application of an area of pure mathematics to the solution of problems in other fields. Practical mathematics is, as already stated above, mathematics that evolves whilst working on problems in a variety of field, which are susceptible to mathematical solutions. This is, of course, the province of the Renaissance Mathematicus the eponym of this blog, and as I wrote in an earlier blog post, Why Mathematicus?

If we pull all of this together our Renaissance mathematicus is an astrologer, astronomer, mathematician, geographer, cartographer, surveyor, architect, engineer, instrument designer and maker, and globe maker. This long list of functions with its strong emphasis on practical applications of knowledge means that it is common historical practice to refer to Renaissance mathematici as mathematical practitioners rather than mathematicians.

One major area of practical mathematics that bloomed and flourished in the Renaissance was surveying, as I described in detail in a post in my Renaissance science series. The root word survey has over the centuries acquired many different meanings, but it has a visual origin from the Medieval Latin supervidere “oversee, inspect,” from Latin super “over” plus videre “to see”. Renaissance land surveying is totally dependent on line-of-sight observations. The legendary straight Roman roads were so straight because the engineers laid them out from high point to high point by line of sight and then instead of going around obstacles cut through them, bridged them or whatever. Triangulation, the major advance in surveying that emerged during the Renaissance, also relies on direct line-of-sight observation from high point to high point to construct its triangles. 

What, however, happens when you need to survey a territory were you literally can’t make direct line-of-sight observations? This is exactly the problem that had to be solved with the massive expansion in metal ore mining that took place during the Renaissance in eastern Europe. To solve it the miners developed their own form of practical mathematics that became known as Markscheiderkunst and its practitioners as Markscheider. Thomas Morel has written a fascinating and highly informative book, Underground Mathematics: Craft Culture and Knowledge Production in Early Modern Europe^[1] that investigates the origins and evolution of this branch of practical mathematics from its origins up to the beginning of the nineteenth century. 

The terms Markscheider and Markscheidekunst are German and Morel’s book concentrates on the mining history of the mining regions in Eastern Germany because that is where the then modern mining industry developed and as Morel explains the knowledge that the German miners developed was then exported all over Europe. If you wanted to start your own mining endeavours, you imported German miners. As I explained in an earlier post this is why Nürnberg developed into a major centre for the manufacture of pencils. Miners in the service of Nürnberg companies were drafted into Borrowdale in Cumbria to exploit the recently, by accident, discovered graphite deposits in the sixteenth century and brought back the knowledge of this new writing material with them when they returned home to Nürnberg. 

The Markscheidekunst, ‘the art of setting limits’, comes from the German words Mark, here with the meaning of boundary, and Scheiden meaning separate, so it means the setting of boundaries, originally between mining claims and the Markscheider is the surveyor, who determines those boundaries. On the surface, no different to other surveying but determining the same boundaries under ground becomes a whole different problem, which led to the Latin translation of Markscheidekunst, geometria subterranea.

The obvious difference between the German Markscheidekunst a term of the Bergmannsprache (the miners’ dialect) and the scholars’ Latin term geometria subterranean displays a divergence between the two worlds that illustrates one of the central theses of Morel’s narrative, which begins in the first chapter.

Morel starts there where somebody, like myself, with only a superficial knowledge of Renaissance metal ore mining would expect him to start with Agricola’s De Re Metallica. The first chapter covers both the publications on mining of Georgius Agricola (1494–1555) and of Erasmus Reinhold the Younger (1538–1592), the son of the famous astronomer, Erasmus Reinhold the Elder (1511–1553). Both authors were humanist Renaissance scholars writing in Latin and Morel shows that their presentations of underground surveying don’t match with the reality of what the Markscheider were actually doing. More generally the work of the Markscheider in the Bergmannsprache was largely incomprehensible to the educated scholars. 

Morel’s second chapter goes into the detail of how the Markscheider actually went about their work. Firstly, how mining claims were staked out above ground and secondly how they measured and mapped the underground mine galleries, which followed the twist and turns of the veins of metal ore. Also, how they ensured that the underground galleries didn’t extend beyond the boundaries of the claim staked out on the surface. The Markscheider developed a practical mathematical culture that was substantially different from the learned mathematical culture of the university-trained scholars. In the early decades, the world of the Markscheider was, like other trades, one of an oral tradition with apprentices learning the trade orally from a master, who passed on the knowledge and secrets of the trade. Morel traces the evolution of this oral tradition and also the failure of university trained mathematicians to comprehend it

Despite their differences to their learned colleagues in the sixteenth century, because of the economic importance of the metal ore mines the Markscheider acquired a very high social status and achieved standing at the courts in the mining districts. They became advisers to the aristocratic rulers and their expertise was requested and applied in other areas of mathematical measurement such as forestry. All of this is dealt with in detail in Morel’s third chapter. 

The seventeenth century saw the development of a scribal tradition with the appearance of the manuscript Geometria subterranea or New Subterranean Geometry, allegedly written by the mining official Balthasar Rösler (1605–1673). These manuscripts evolved over the century as did the methods of surveying and the instruments used by the mine surveyors. Surprisingly this literature remained in manuscript form for most of the century only appearing in print form with Nicolaus Voigtel’s Geometria subterranea in 1686. In his fourth chapter, Morel gives a detailed analysis of this manuscript tradition and offers and explanation as to why it remained unprinted, which has to do with the way these manuscripts were used to train the apprentice surveyors.

Chapter five takes into the late seventeenth early eighteenth centuries, following the publication of Nicolaus Voigtel’s Geometria subterranea and the life and work of Abraham von Schönberg (1640­–1711), Captain-general of the Saxon mining administration, and his endeavours to revive the local mining districts in the aftermath of the Thirty Years War. Central to Schönberg’s efforts was the development of the mining map of which the most spectacular example in the Freiberga subterranea, a gigantic cartography of the Ore Mountains running continuously over several hundred sheets. Ordered by Schönberg and realised by the surveyor and mine inspector, Johann Berger (1649–1695). 

First sheet of the Freiberga subterranea

Morel’s sixth chapter takes the reader into the eighteenth century and the attempts to raise the academic level of the mathematical knowledge of the mine surveyors and engineers leading up to the establishment of the Bergakademien (in English, mining academies). As Morel explains these were initially not as successfully as might be supposed. Morel takes his reader through the problems and evolution of these schools for mine surveyors. He also follows the significant developments made outside such institutions, particularly by Johann Andreas Scheidhauer (1718–1784). A recurring theme is still the inability of university educated mathematicians to truly comprehend the work of the practical mathematicians in the mining industry. As Morel writes at the beginning of his summary of this chapter, “Teaching a mathematics truly useful for the running of ore mines was a daunting task that underwent important transformations during the eighteenth century.”

Morel’s final chapter is dedicated to the story of the Deep-George Tunnel, a 10 km long drainage tunnel at a depth of 284 m, which connected up numerous mines in the Harz mining district. An extraordinary project for its times. Morel shows how the planning, for this massive undertaking, was based on data recording techniques for the run of the mine galleries developed in the preceding centuries rather than new surveying. The theoretical planning was on a level not previously seen in ore mine surveying. Morel also describes in detail an interesting encounter between the practical mining engineers and a theoretical scientist. The Swiss scholar Jean-André Deluc (1727–1817) visited the area in 1776, just before the start of the project, to test the calibration of his barometers to determine altitude by descending into the depths of the mine, having previously calibrated them by ascending mountains. Impressed by the undertakings of the mining engineers he returned several times over the years observing the progress of the tunnel and reporting what he observed to the Royal Society of London. 

The story of the Deep-George Tunnel is a very fitting conclusion to Morel’s narrative of the evolution of the practical mathematical discipline of subterranean surveying in the ore mines of eastern Germany. The breadth and depth of Morel’s narrative is quite extraordinary and my very brief outlines of the chapters in no way does it justice, to do so I would have to write a review as long as his book. Morel is an excellent stylist, and his book is a real pleasure to read, a rare achievement for a highly technical historical text. There are extensive footnotes packed with sources and information for further reading. There is an almost thirty-page bibliography of manuscript, printed primary, and printed secondary sources, and the book closes with an excellent index. The book is nicely illustrated with grayscale reproductions of original diagrams.

This is truly a first-class text on an, until now, relatively neglected branch of practical mathematics, which should appeal to anyone interested in the history of mathematics or the history of mining. It will also appeal to anybody interested in a prime example of the narrative history of a technical disciple that combines mathematics, technology, politics and economics. 

---

^[1] Thomas Morel, Underground Mathematics: Craft Culture and Knowledge Production in Early Modern Europe, Cambridge University Press, 2023.

Renaissance science – XLI

The cabinets of curiosity featured in the last episode of this series often featured a section containing a mixed collection of stones, minerals, and fossils all thrown together in one category of natural history. This is not surprising when one thinks that the word fossil originally meant anything dug up out of the ground, from the Latin fossilis meaning dug up, and only acquired its modern meaning at the beginning of the eighteenth century. This is wonderfully illustrated by the fact that the first published description of a pencil is in Conrad Gessner De Omni Rervm Fossilivm Genere (1565), graphite being something that is dug up.

Whilst not necessarily to the extent that modern botany was formed by the Renaissance, the three disciplines of palaeontology, mineralogy, and geology also began to gradually emerge during the Renaissance. 

As with the other areas of natural history the Renaissance interest in things out of the earth begins with the recently published books from antiquity. Aristotle (384–322 BCE) wrote about the properties of minerals in terms of his general four element theory of all known substances. Theophrastus (370–285 BCE), Aristotle’s pupil and successor as head of the Peripatetic school, followed Aristotle in dividing minerals into two categories–those affected by heat and those affected by dampness–in his De Mineralibus. Theophrastus’ knowledge of a wide range of substances was quite extensive. He knew that both amber and magnetite had powers of attraction, that pearls came from shellfish, and that coral comes from India. He also knew about coal and the metal ores, and that pumice stone is volcanic in origin. He knew about the practical use of various minerals in production of glass, pigments, and plaster. He also describes precious stones. He is aware that minerals often come from mines and discusses gold, silver, and copper mines. He apparently also wrote a separate work On Mining, which is lost.

As is almost always the case, Theophrastus’ wide-ranging work on minerals is overshadowed by the much more extensive writings of Pliny (23/24–79 CE) in his Naturalis Historia in which books 33 to 37 in volumes IX and X are devoted to mining and mineralogy, especially as applied to life and art, work in gold and silver, statuary in bronze, art, modelling, sculpture in marble, precious stones, and gems. He describes many more minerals than Theophrastus, discussing their properties and applications. He was the first to recognise the correct origin of amber.

The other driving force, during the Renaissance, behind the increased interest in things out of the earth was the development of a major mining industry in Middle Europe for the extraction of metal ores. These developments are reflected in the publications of two significant and successful books on the practice of mining, the Pirotechnica of the Italian mining engineer, Vannoccio Biringuccio (1480­–1539), published posthumously in 1540 and De re metallica by the German physician Georgius Agricola (1494–155), also published posthumously in 1556.

Book I of Biringuccio’s Pirotechnica is titled Every Kind of Mineral in General and deals with the location of metal ores and deals separately with the ores of gold, silver, copper, lead, tin, and iron. Book II continues the theme with what Biringuccio calls the semi-minerals an extensive conglomeration of all sorts of things that we wouldn’t necessarily call minerals. Starting with quicksilver he moves on to sulphur then antimony, marcasite (which includes all the sulphide minerals with a metallic lustre), vitriol, rock alum, arsenic, orpiment, and realgar. This is followed by common salt obtained from mine or water and various other salts in general then calamine Zaffre and manganese. As with Theophrastus he also, under minerals, deals with loadstone, Theophrastus’ magnetite.

In Book I of De re metallica, Agricola deals with the industry of mining and ore smelting, moving on to finding minerals and metal ores in Book II. Book III discusses mineral veins and seams. After several books which discuss the smelting of various metal ores, the final Book XII, discusses salts, solvents, precipitates, and glass. 

Source: Wikimedia Commons

Unlike Biringuccio, who only discussed minerals in the context of his book on mining, Agricola wrote and published several other works on minerals. His earliest publication on mining Bermannus sive de re metallica dialogue (1530) also contained much on mineralogy, as did his De animantibus subterraneis (1549).

However, his major work was his De natura fossilium published in 1546; here the word fossil is used in the sense of things out of the earth. In the ten books of this work, he combined the extensive knowledge about fossils, minerals, and gemstones passed down from antiquity and the Middle Ages with the oral, vernacular, practical, traditional experience of the mineworkers, smelters, and stone masons about the occurrence, exploitation, appearance, structure, properties, and uses of those things found underground.

Title page of De natura fossilium Source: Wikimedia Commons

Anselmus de Boodt (1550–1632), who we met as the curator of the cabinet of curiosities of Rudolf II in Prague, was as a natural historian principally interested in cataloguing all know stones and mineral, a task to which he devoted a large part of his life.

Engraved Portrait of Anselmus Boetius De Boodt by Egidius Sadele Source: Wikimedia Commons

The results of his endeavours were published in Latin in his Gemmarum et Lapidum Historia (The History of Gems and Stones), the first edition, dedicated to Rudolf, appearing in Hanau in 1609. Two further editions appearing in Leiden in 1636 and 1647.

Title page of the Gemmarum et Lapidum Historia Source: Wikimedia Commons

The third and final edition of 576 pages was in two parts. The first part gave the various causes of minerals, heavily influenced by the Work of Aristotle and Theophrastus but nevertheless giving providing unique accounts of how minerals are formed. The second part catalogues methodically hundreds of specific minerals, describing in detail their various identifying and curative properties. 

Another specialist for minerals and fossils, who we met as curator of a cabinet of curiosities was Michele Mercati (1541–1593), who served the pope in this function as well as directing the Vatican botanical garden.

Portrait of Michele Mercati, artist unknown Source: Wikimedia Commons

The emphasis of his collection lay in stones, minerals, and fossils. Based on his work, he wrote his Metallothica. Opus postumum, auctoritate et munificentia Clementis undecimi pontificis maximi e tenebris in lucem eductum; opera autem et studio Joannis Mariae Lancisii archiatri pontificii illustratum, which, however, was first published in Rome in 1717. Mercati was one of the first to recognise that the chipped flints in his collection were not, as believed at the time, produced by lightning but were tools produced by humans. 

Engraving made by Antonio Eisenhot between 1572 and 1581, but published in 1717, representing the Vatican mineral collection as organized by Michele Mercati Source: Wikimedia Commons

The sixteenth century’s perhaps greatest natural historian, Ulisse Aldrovandi (1522–1605), also had a very substantial collection of minerals, fossils, and stones in his teatro di natura (theatre of nature), and he of course wrote about them, although his text on the topic was one of those unpublished at the time of his death and the eventual late publication of his monumental Musæum Metallicum in 1648, certainly affected its reception, giving it not the attention it deserved. Already in his will in 1605, Aldrovandi was the first to use the word giologia (geology) in the modern sense, although his introduction had little impact, the usage first becoming widespread in the eighteenth century. Previously the word geologia had been used to distinguish earthly philosophy from theology. 

Body fossils pictured in the Musaeum Metallicum. A. Aldrovandi describes this specimen as a ” rock pregnant with a shell. ” Aldrovandi considers most fossils to be of inorganic origin made in imitation of living beings. B. Although Aldrovandi believes that fossils are not of organic origin, he often compares them to existing animals. He calls this structure ” Rhombites, ” meaning a ” (stone) resembling a fish of the Rhombus kind. ” C. Detail from the plate entitled ” belemnitarum septem differentiae ” (seven varieties of ” belemnites ” ). D. Aldrovandi calls shark teeth ” glossopetrae, ” or ” tongue-like stones. ” This specimen is given the attribute ” Gesneri, ” or ” Gesner’s ” : naturalist Konrad Gesner (Gesner, 1565) had already described shark teeth as ” Glossopetre ” in 1565. E. Aldrovandi often calls echinoderm fossils ” astroitis, ” a word that comes from the Latin ” aster, ” meaning star. The ” star-echinoderm ” comparison is most likely based on echinoderms’ pentameral symmetry, resembling the stylized figure of a star. The comparison was already made by Gesner (1565) in his description of fossil crinoids similar to those depicted by Aldrovandi and shown here. F. Aldrovandi frequently uses the term ” ophiomorphites, ” or ” snake-like stones, ” in his descriptions of ammonites. G, H. Fossil sea urchins, presented as ” astroitis ” (see E). I. When describing this mammoth tooth, Aldrovandi speaks of ” petrifaction. ” See also Vai and Cavazza (2006, fig. 14) J. Fossil coral, also presented as ” astroitis ” (star-stone), presumably because of the polyps’ stellate morphology. K. Aldrovandi distinguishes two main types of ” glossopetre ” : dentate (as in D) and nondentate (as in K).  Source

In his Musæum Metallicum, rather than simply listing the minerals etc, Aldrovandi attempts to apply a systematic classification to the objects under examination. He appears to be clearly aware of the organic original of fossils; Aristotle had claimed that fossils were stones that grew in the ground and only imitated organic forms. Aldrovandi was the first to recognise and describe microscopic fossils on the surface of a calcareous marble-like block: He almost certainly used a magnifying lens to do so. Aldrovandi’s work was in many senses highly innovative but had little impact, his various discoveries being remade by later researchers.

The other mega Renaissance natural historian, Conrad Gessner (1515–1565), also, as already noted above, also wrote and published a substantial work in the year of his death, his De Rerum Fossilium, Lapid um et Gemmarum maxime, figuris et similitudinibus Liber: non solum Medicis, sed omnibus rerum Naturae ac Philogiae studiosis, utilis et juncundus futurus, usually simple referred to as Fossils, Gems, and Stones. Although, he didn’t recognise the true origin of fossils, he did realise that their unusual appearance deserved recognition, and his book contains the earliest extensive collection of fossil illustrations. 

Fossil illustrations from ‘De omni rerum fossilium’, showing shark’s teeth Source: Welcome images via Wikimedia Commons ( you can read more about Gessner’s fossil book with more illustrations including that pencil, here)

Gessner was not the first to published illustration of fossils, that honour goes to the German Lutheran rector Christoph Entzelt (1517–1583), who published a De Re Metallica: Hoc Est, De Origine, Varietate, & Natura Corporum Metallicorum, Lapidum, Gemmarum, atq[ue] aliarum, quae ex fodinis eruuntur, rerum, ad Medicinae usum deseruientium, Libri III, under the name Chistophorus Encelius, in 1557, which contains illustrations of four fossils. I have been unable to find out any more about Entzelt or his book.

Source

Like Aldrovandi, Gessner tried to systemise his presentation of the objects describe in his book by dividing them up into fifteen classes. However, his classifications were, by modern standards, trivial and or illogical and had very little influence on the developments within the disciplines of mineralogy, geology, or palaeontology.

In their books on the mining industry both Biringuccio and Agricola drew attention to stratigraphy, the layers under the surface of the earth playing a significant role in the practice of mining. Whilst discussing the types of layers that would potentially lead to fruitful seams of whatever was being mined in a given situation, they gave no thought as to how they various layers came into existence. The first scholar to do so was the Danish anatomist, palaeontologist, and geologist Niels Steensen (1638­–1686), more generally known by the Latin version of his name as Steno. 

Portrait of Niels Steensen (1666–1677). Unsigned but attributed to court painter Justus Sustermans. Source: Wikimedia Commons

Born in Copenhagen, he studied medicine at Copenhagen University. After graduating he travelled first to Rostock and then on to Amsterdam and further to Leiden, where he studied anatomy together with Jan Swammerdam (1637–1680), Frederik Ruysch (1638–1731), Reinier de Graaf (1641–1673), and Franciscus de le Boe Sylvius (1614–1672). As an atomist he made important discoveries and contributions.

After travelling through France, he settled in Italy where he became a member of the Accademia del Cimento. Here, he first made a major contribution to palaeontology and then one to geology. In 1666, he dissected a female shark’s head and recognised the similarity between the shark’s teeth and the fossils known as glossopetrae or ‘tongue stones.’ Steno published his theories that fossils are organic material turned into stone in his Canis carchariae dissectum caput in 1667.

Elementorum myologiae specimen: Illustration from Steensen’s 1667 paper comparing the teeth of a shark head with a fossil tooth. Source: Wikimedia Commons

Previously, the Italian naturalist and botanist Fabio Colonna (1567–1640) had in his investigations found evidence that glossopetrae had organic origins, which he published in his De glossopetris dissertatio in 1616.

Portrait of Colonna 1572 artist unknown Source: Wikimedia Commons

Source:

Whilst walking along the coast in Northern Italy Steno began to take interest in the exposed layers in the earth. He developed theories of stratigraphy defining four laws or principles of how the layers came into being, which he published in his De solido intra solidum naturaliter contento dissertationis prodromus (Preliminary discourse to a dissertation on a solid body naturally contained within a solid) in 1669.

Source: Wikimedia Commons

Steensen, in his Dissertationis prodromus of 1669 is credited with four of the defining principles of the science of stratigraphy. His words were:

1. The law of superposition: “At the time when a given stratum was being formed, there was beneath it another substance which prevented the further descent of the comminuted matter and so at the time when the lowest stratum was being formed either another solid substance was beneath it, or if some fluid existed there, then it was not only of a different character from the upper fluid, but also heavier than the solid sediment of the upper fluid.”
2. The principle of original horizontality: “At the time when one of the upper strata was being formed, the lower stratum had already gained the consistency of a solid.”
3. The principle of lateral continuity: “At the time when any given stratum was being formed it was either encompassed on its sides by another solid substance, or it covered the entire spherical surface of the earth. Hence it follows that in whatever place the bared sides of the strata are seen, either a continuation of the same strata must be sought, or another solid substance must be found which kept the matter of the strata from dispersion.”
4. The principle of cross-cutting relationships: “If a body or discontinuity cuts across a stratum, it must have formed after that stratum.” 

(Taken from Wikipedia)

Somewhat bizarrely Steno converted from the Lutheran Protestantism of his birth to Catholicism in 1667. He was ordained a priest in 1675. He was consecrated bishop in 1677 and went off to Lutheran North Germany as a missionary. Living in poverty he died in 1686 after severe illness. In 1988 he was beatified by Pope John Paul II.

Portrait of Steno as bishop (1868) Source: Wikimedia Commons

Although, the full development of palaeontology, geology, and minerology didn’t take place until the eighteenth century, during the Renaissance the first steps were taken in separating and defining the three as individual disciplines.